class: inverse, bottom, right <!--- About macros.js: permite escalar las imágenes como [:scale 50%](path to image), hay si que grabar ese archivo js en el directorio. .pull-left[<images/Conocimiento cívico.png>] .pull-right[<images/Conocimiento cívico_graf.png>] ---> # __Cuarta Clase Métodos Cuantitativos II__ ## *Principios de la causalidad y análisis de correlación* <br> <hr> ### Docente: Francisco Meneses ### Ayudante: Victoria Arias <br> --- class: inverse, middle, center, slideInRight # Entre la causalidad y la correlación --- ## Correlación vs. causalidad - La correlación **no implica causalidad**. - Para hablar de causalidad se requieren **tres condiciones**: A) **Temporalidad**: La causa es anterior al efecto. -- B) **Asociación**: existe relación estadística entre A y B. -- C) **No espurias**: no existen otros factores que expliquen la asociación. --- ## Ejemplos de errores: Problema temporal. - **Error de incoherencia temporal** Ejemplo: *Los piojos alejan las enfermedades - Cuando en realidad el tener fiebre aleja los piojos*. -- - **Error de falta de Asociación** Ejemplo: *Las vacunas del COVID generan infertilidad - Cuando no existe evidencia de que la gente vacunada con COVID-19 sea menos fértil que la gente no vacunada*. -- - **Error de variable alternativa (correlación espuria)** Ejemplo: *El aumento de la vacunación ha aumentado los niveles de autismo - Ambas cosas se deben a una expansión de los servicios médicos*. Otros ejemplos: feminismo-violencia, helados-ahogos --- # El rol de los experimentos * Son una evaluación confiable de causalidad * Son situaciones controladas * Nos dan seguridad de no espuriedad (por aleatorio) * Difíciles de aplicar en la practica 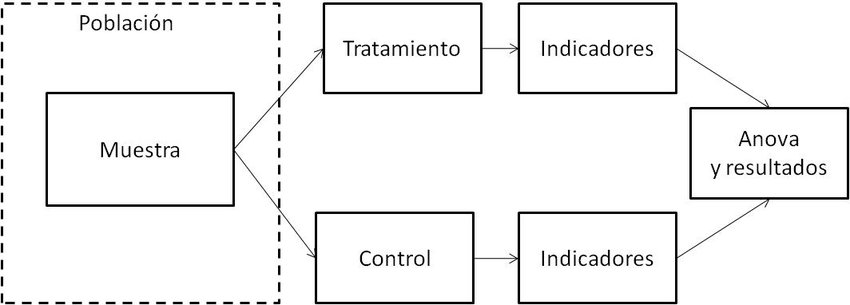 --- # En suma... * Comprobar causalidad requiere de tres supuestos: temporal, asociación, no espuriedad * La correlación no implica causalidad, pero es una condición de ella * Los experimentos son una forma confiable de causalidad, pero poco prácticos en CCSS --- class: inverse, middle, center, slideInRight # Cómo medimos la correlación --- ## El índice de correlación de Pearson - Mide la **intensidad y dirección** de la relación lineal entre dos variables. - Sus valores están entre -1 y 1. **Interpretación: ** - +1 → relación lineal positiva perfecta. - -1 → relación lineal negativa perfecta. - 0 → ausencia de relación lineal. 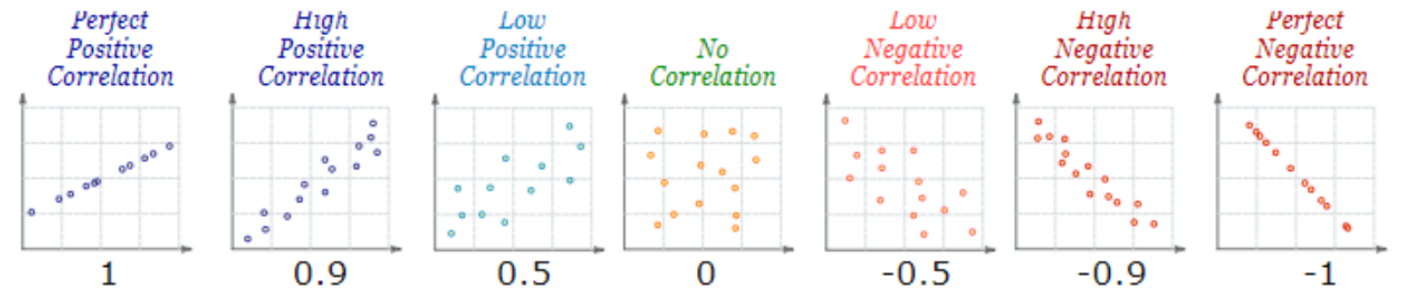 --- class: inverse, middle, center, slideInRight # ¿Cuándo usamos la correlación de Pearson? --- ## Condiciones de las variables - Ambas variables deben ser **cuantitativas** (numéricas continuas o de intervalo/razón). - Relación **lineal** entre las variables. - Distribución aproximadamente **normal** de cada variable. - Homocedasticidad: la dispersión de los valores debe ser similar a lo largo del rango. - No debe haber **outliers extremos** que distorsionen la relación. --- ## Consideración clave - La correlación de Pearson **no establece causalidad**. - **No propone dirección temporal**: - No podemos afirmar si A causa B o B causa A. - Solo indica que **ambas se mueven juntas** en cierta medida. --- # Lectura del coeficiente r A) **Significación** - Se contrasta con un test estadístico para evaluar si la correlación es distinta de 0. B) **Dirección** - El signo (+/-) de r indica si la relación es positiva o negativa. C) **Fuerza** - |r| cercano a 1 = relación fuerte. - |r| cercano a 0 = relación débil. > La fuerza nos indica cuanto se ajustan los puntos a la línea, no la pendiente --- # Ejemplo aplicado (conceptual). - Supongamos que obtenemos un coeficiente de correlación de **r = 0.84** con 30 observaciones. - El p-valor < 0.001 indica que la correlación es **estadísticamente significativa**. - Interpretación: existe una relación positiva fuerte y confiable entre las variables. --- # Ejemplo de correlación débil/no significativa - En otro estudio, se obtiene un coeficiente de correlación de **r = 0.05** con 30 observaciones. - El p-valor = 0.81 → la correlación **no es estadísticamente significativa**. - Interpretación: no hay evidencia suficiente para afirmar que exista relación en la población. --- # Tabla de referencia sobre magnitud de r | Valor de r (absoluto) | Interpretación | |-----------------------|----------------| | >0.10 | Débil | | >0.30 | Moderada | | >0.50 | Fuerte | *(Los puntos de corte son orientativos, no reglas estrictas.)* --- <!-- --> --- ``` r # Cálculo de Pearson cor.test(x, y, method="pearson") ``` ``` ## ## Pearson's product-moment correlation ## ## data: x and y ## t = 7.549, df = 28, p-value = 3.189e-08 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## 0.6504985 0.9105192 ## sample estimates: ## cor ## 0.8188633 ``` --- ``` r # Visualización df <- data.frame(x, y) sjPlot::plot_scatter(df,x,y, fit.line="lm") ``` ``` ## `geom_smooth()` using formula = 'y ~ x' ``` 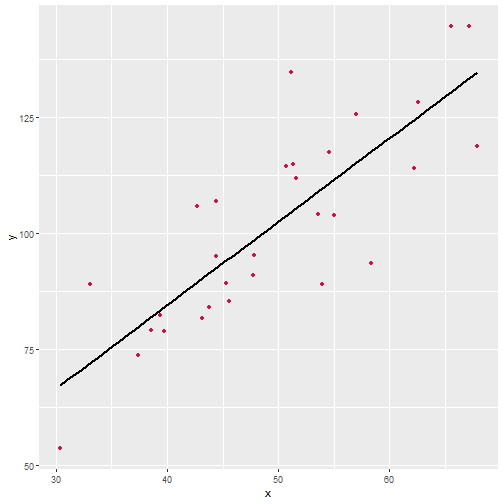<!-- --> --- [https://www.guessthecorrelation.com/](https://www.guessthecorrelation.com/) --- .center[ <img src="images/qr-code.png" width="60%"> ]